Stealth in Space

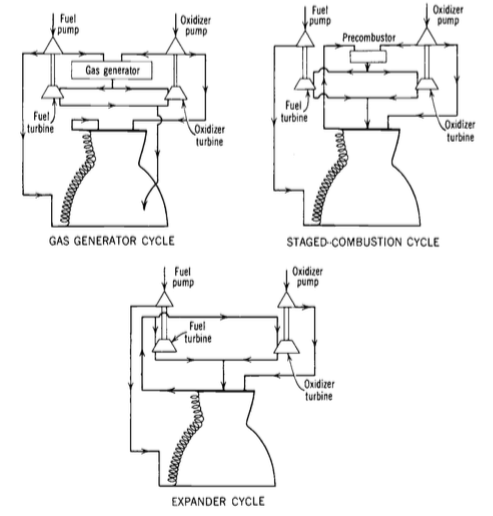
Few concepts of space warfare have inspired as much controversy (and hate mail) as discussing stealth in space, so I figured it’s time to have an article about that.

The bright Apollo 8 plume observed from Earth, as it makes a Trans-lunar Injection.

For starters, though, I’d recommend checking out Winchell Chung’s website, Atomic Rockets, which has an excellent discussion on this topic, aptly titled There Ain’t No Stealth in Space. I will summarize the main points about stealth here, but for an in-depth discussion of them, see the above link.

• Carefully scanning the entire celestial sphere takes 4 hours or less.
• Thruster burns of any drive with reasonable power can be detected all the way across the solar system (billions of km away).
• Even with engines cold, the heat from radiators attached to life support will be detectable at tens of millions of km away, which is still far too large to get any sort of surprise.
• Radiating heat in a single direction (away from the enemy) is easily defeated by fielding a number of tiny detector probes which idly coast about the system. Additionally, the narrower of a cone in which you radiate heat, the larger and larger of radiators you need to field. A 60 degree cone of radiation is roughly 10% as efficient, and it only gets worse the tighter of a cone you have.
• Making a huge burn and then trying to stealthily coast for months to the target is do-able, but as long as your enemy can track your first burn, they can very accurately predict where you’ll be as you coast across the solar system. And you still have to worry about radiating your heat for months.
• Decoys are only really viable on really short time scales, such as in combat. Over the long term, study of a decoy’s signature over time will reveal it’s true nature. It would need a power source and engine identical to the ship it’s trying to conceal, as well identical mass, otherwise the exhaust plume will behave differently. This means your decoy needs to be the same mass, same power, same engine as your real ship, so at that point, why not just build a real ship instead?

Anti-stealth detection measures was developed heavily during the cold war for detecting ICBMs. In space, without a horizon or an atmosphere, it’s far easier.

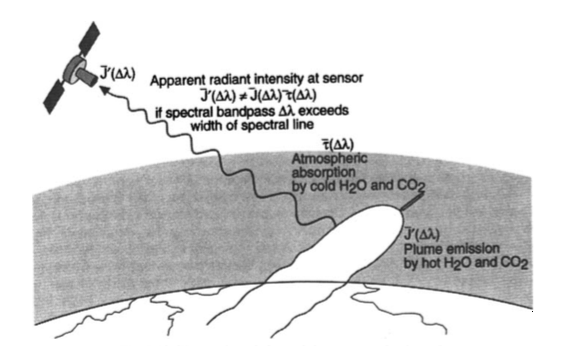
There are a few more points that are not mentioned but I get messaged about them a lot, so I’ll put them here.

• Hiding behind a planet to make a burn is not really feasible. All it takes is two detectors at opposite sides of this planet to catch this. In reality, a web of tiny, cheap detectors spread across the solar system will catch almost all such cases.
• A combat-ready ship will require very hot radiators for its nuclear powerplant for use in combat. If these radiators are going to be completely cold for the journey, they will suffer enormous thermal expansion stress when activated. In order to avoid this, very exotic and expensive materials for your radiators will be needed to get from 10 K to 1000 K without shattering. Not only that, your radiator armor will need to be similarly exotic, which means it will likely not be very good at armoring your radiators anyways.

Rocket exhaust plumes can be uncoupled from atmosphere using modern technology after some study. This step can be skipped in space.

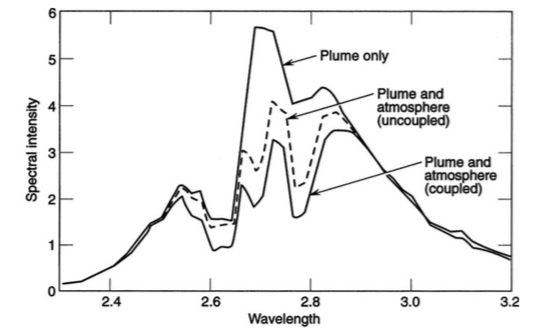
Now there are plenty of dissenting views (as Atomic Rockets is good to point out, as well as rebuttals to the rebuttals). Certain partial solutions, such as using internal heatsinks, and so on, are pointed out, but they all are very limited.

Ultimately, stealth in space is somewhat possible, but current proposed solutions are either ridiculously expensive, impractical, or require you to accept limitations that defeat the purpose of stealth in the first place. Indeed, rather than consider it a ‘yes-or-no’ question, it’s simply a matter of how close you can get to the enemy before they detect you.

In practice, ‘how close’ generally means halfway across the solar system, with expensive stealth solutions reducing that distance only partially. Given this, Children of a Dead Earth runs with the assumption that stealth is not a reasonable military tactic for near future space warfare.

But let’s look at an example of possible stealth: replacing your main engine (nuclear rocket or combustion rocket) with a solar sail. Your exhaust plume is now nonexistent, but now you have to take decades to centuries deliver a military payload anywhere (troops or weaponry). Your best bet is to keep your payload very small if you want to get anywhere in reasonable time. And you still have to worry about your radiators.

Concept art of a solar sail. Abysmal thrust, and basically useless in the outer solar system, but it’s stealthy.

Suppose replace your crew module with basic electronics, and do away entirely with the crew and their hot radiators. This is reasonable for any short term space travel, but over the course of months where things can and will go wrong with the ship or the strategic situation, having a human element is necessary. Alternatively, if Strong AI can be developed, this is another possible solution, but this assumes that such an AI won’t require lots of power and heat to radiate as well.

A different idea to get around this problem is to put everyone in cryosleep and keep the ship basically frozen. Comes with a host of it’s own problems as well, chiefly that the technology does not exist yet.

Given a solar sail and crewless ‘dumb’ ships with miniature payloads, you can build ships that can sneak across the solar system and do very little. Such ships would be unable to respond to complex and unexpected tactical decisions, and would be very easy to outsmart, as well as easy to spoof with electronic warfare. They could perhaps be used as mines, given a tiny amount of a delta-v and a small nuclear payload.

Ironically, this specification of tiny, ‘dumb’ stealth crafts is exactly what you need to build a web of detectors scattered about the solar system. This means the field of cheap detectors you want spanning the solar system can be created stealthily.

The Hubble Space Telescope. Much smaller and cheaper versions can be scattered about the solar system stealthily if using solar sails.

Defensive stealth in space exists in full force. When you enter orbit of an the enemy’s planet, they might have an inordinate amount military hardware and spacecrafts hidden beneath the surface. But as soon as they launch, the secret is out.

This idea plays a major role in Children of a Dead Earth, as when the enemy drops into orbit around your planet, one must always be wary that the enemy fleet is simply trying to draw out your forces to get a tally on what you actually have. This constantly requires balancing of launching just enough firepower to deal with the enemy without revealing too much about one’s own reserves.

A Titan Missile Silo from the cold war. Similar silos could be littered across planets, moons, and asteroids with full fledged capital ships, ready to launch when the enemy enters low orbit.

The easiest way to conceal a large amount of military hardware for a long distance invasion is to hide it amongst commercial traffic. Of course, this requires complicity with the civilian traders, either bought with money or intimidation, but it is possible. And such perfidy also plays a key role in Children of a Dead Earth.

With that all in mind, I will admit that at the beginning of my project, I was dead set on getting stealth to work in space warfare. Ultimately, I came to the conclusion that while stealth in space is certainly possible, it is not feasible given mass, cost, and time constraints. If you want stealth, you need to pay the price of decades-long travel times, enormously massive ships, vastly reduced military effectiveness, or all of the above all at once.

At the beginning of the project, I did explore some more exotic solutions to stealth, but I ultimately wasn’t keen on implementing technologies that were not heavily reviewed and published in scientific articles. At some point though in future posts, I will go over all of the more ‘out there’ technologies I considered for all aspects of space warfare (like a hypothetical nuclear rocket which generates an exhaust plume at 30 K, for instance). Stay tuned!

The Photon Lance

We’ve looked into mass weapons, now let’s take a peek at lasers.

A laser firing. This one is visible when fired within the atmosphere.

Comparatively, lasers are far more complex than any of the weapon designs we’ve looked into, with far more components and considerations.

For example, in module design, railguns and the like can be optimized by simple tweaking and trial and error. On the other hand, it is very difficult to do so when designing lasers. The relations between the inputs and outputs are not only nonlinear, they are absolutely not monotonic, so simply using trial and error to find ideal cases is not always possible.

While there was an explosion of different design options and choices for railguns as we saw in Origin Stories, with lasers, it was far worse. First you’ll choose your laser type from amongst a staggering array of types. Then you’ll need a pumping source, which includes a nearly infinite number of pumping and lasing geometries, each with different advantages. And you’ll probably want to add a nonlinear crystal to harness Frequency Switching in order to double, triple, or quadruple your photon frequency.

All the laser inputs you can tweak on the right, and the outputs on the left.

Then you need to worry about the optics between each and every subsystem, ensuring the photons don’t seriously damage each lens, mirror, or nonlinear crystal at each point. Plus, you need to arbitrarily focus your beam at different distances, either with a Zoom Lens or with a Deformable Mirror (though in practice, zoom lens tend to be impractical for extremely long ranges, meaning you’re usually stuck with using a deformable mirror).

Also, and if you want to pulse your laser, you’ll need to use Mode Locking, Q Switching, or Gain Switching to do so. Finally, while mechanical stress are basically irrelevant for lasers (recoil of lasers is minuscule), thermal stresses are huge. Cooling your laser effectively is one of the most important parts of building a working laser.

Laser construction is not for the faint of heart, but the outputs of lasers are actually fairly simple compared to mass weapons. While mass weapons produce a projectile of varying dimensions and materials at a certain speed, possibly with excess temperature, and possibly carrying a complex payload, lasers just shoot a packet of photons. Even if the laser is continuous, the beam fired can be considered series of discrete packets.

Simplified diagram of laser ablation effects.

Since laser beams move at the speed of light, it is actually impossible to dodge a laser unless you are always dodging. This is because the speed of light is the speed at which information travels in the universe. Thus, you can never determine where a laser will be until it actually hits you. This would be impossibly overpowered in warfare were it not for diffraction.

A packet of photons is focused on a single point of a certain size, and carries a discrete amount of energy of a single wavelength/frequency. Technically, due to quantum mechanics, particularly the Uncertainty Principle, there will be many different wavelengths, an uncertain size, and an uncertain amount of energy. These quantum effects are glossed over because approximating the entire packet as a discrete bundle is both simpler and still remains very close to reality.

The only quantum effect that significantly affects the output of a laser in terms of warfare is Diffraction.

Diffraction pattern of a red laser passing through an aperture.

Diffraction causes a laser beam to diffuse the further it gets from its exit aperture, spreading out the energy of the laser. This is a problem because the energy a beam carries is not what inflicts damage. The energy per unit area, or Fluence, is what causes damage. For continuous beams, it would be the power per unit area, or Irradiance.

A hypothetically perfect laser will suffer from diffraction and is referred to as being Diffraction Limited. But this is not what is actually limits most actual high powered lasers in warfare.

Most high powered lasers will never even come close to being diffraction limited.

Truth is, the Beam Waist, or the minimum diameter the beam will achieve, is a more effective measurement of how damaging a laser is. A perfect laser will have a beam waist limited only by diffraction, but lasers like that don’t exist. And the greater the power of a laser, the further and further away that laser strays from being diffraction limited.

The Beam Waist is twice of

A good way to measure this is with the Beam Quality of the laser, or with the M Squared. is the beam quality factor, which can be considered a multiplier of the beam waist. So, an of 5 means the beam waist is 5 times that of a diffraction limited beam. In terms of area, this means the beam is 25 () times the area of a diffraction limited beam, or 25 times as weak. As you can see, having a even in the high single digits will yield beams a far cry from “perfect” diffraction limited beams.

In practice, it is not the pumping efficiency, nor the power supply, nor diffraction, which ultimately limits lasers. It is the beam quality factor. In the end, ends up being the number one limit on laser damage in combat.

In small lasers, close to 1 is easily achieved without issue, but in high power lasers, can easily reach into the millions if not accounted for. This is because generally, scales linearly with laser power.

Each optical component of a laser affects the . In particular, using a deformable mirror to focus a laser at arbitrarily long ranges (such as from 1 km to 100 km) is measured at reducing to between 1.5 to 3. Problematic, but not exactly debilitating.

A high energy laser developed jointly by the US and Israel. Note the deformable mirror it uses for focusing the beam at arbitrarily long ranges.

But the main issue is Thermal Lensing (Note that this is different from Thermal Blooming, which only occurs outside the laser in the presence of an atmosphere). The heating of a laser gain medium generates a thermal lens which defocuses the beam, ultimately widening the beam waist, preventing the beam from focusing properly. Also note that thermal lensing actually occurs in every single optical component of the laser, though it is strongest in the lasing medium.

Thermal lensing increases roughly linearly with input power. This means if you have 1 kW laser with a of 1.5 (which is reasonable), this means dumping 1 MW into that same laser will yield a of about 1500 (going the other way does not work, since can’t be less than 1).

One might try to predict the thermal conditions and add in an actual lens reversing the thermal lens. Unfortunately, the thermal lens is not a perfect lens either, and the imperfections of this lens remain the primary cause of beam quality reduction.

Fiber lasers are often touted as a solution to thermal lensing. They are considered immune to thermal lensing except in extreme cases. Unfortunately, dumping hundreds of megawatts through a fiber laser constitutes an extreme case, and fiber lasers suffer thermal lensing nearly as badly as standard solid state lasers.

Free Electron Lasers (FELs) are a design which do not have a gain medium to suffer thermal lensing in, however they still suffer thermal lensing is all other optical components.

The largest innovation for combating thermal lensing are negative thermal lenses. Most gain mediums have a positive thermo-optic coefficient, and this is what generates the thermal lens. Certain optical materials have a negative thermo-optic coefficient, which produces a thermal lens inverse of what the gain medium produces. Ideally, this negative thermal lens would perfectly reverse the positive thermal lens, but in practice, the still suffers.

In the end, the primary way to combat thermal lensing is with cooling. And the primary way to cool your laser is to make it bigger.

If the proportions of a laser are kept identical, lasers can be scaled up or down with minimal change to the laser’s efficiency or output power. Indeed, you can pump 100 MW or power into a tiny palm-sized laser just as well as you can into a building-sized laser, and they will produce roughly equal beams in terms of efficiency and . The only difference is that the palm-sized laser will melt into slag when you try to fire it.

Laser size is mostly a matter of how much do you need to distribute the heat of the laser pumping. And if you want to combat thermal lensing, you’ll want a really big laser. This means laser size is essentially about cooling, and by extension, having a low .

And because size is closely related to mass, and mass is so critical to spacecraft design, the limiting factor of using lasers in space is how poor of an you want to have, given a certain power level. Though the radiator mass needed for the enormous power supplies is the other major consideration.

For crafts built around high powered lasers, most of the size and mass ends up being the radiators.

A final way to combat thermal lensing is to use Beam Combining of many smaller lasers. Combining beams side by side increases the beam waist linearly, which defeats the point, but Filled Aperture Techniques can combine beams without increasing the beam waist. However, this technique produces greater inefficiency to the final beam. The ideal way to combine beams is to simply use multiple separate lasers which all focus on a single point.

In Children of a Dead Earth, either single large lasers or multiple small, separately focused lasers can be used, and both have varying pros and cons.

Of course, designing lasers in Children of a Dead Earth is often far more difficult than designing any other system, so there are plenty of factory-made options for players to use. But the option is always there for those who really want to explore the depths of laser construction!

What to shoot?

We’ve explored how we launch projectiles at the target (Space Guns), now we will explore what we launch at the target.

Point defense railguns firing tiny 10 gram bullets against a missile salvo.

The simplest projectile is a solid block of mass with a burning pyrotechnic tracer on it. But even a block of mass has several complexities.

The material of a bullet can also be varied to cause for differing effects upon hitting. However, for railguns and coilguns, launching the armature itself is more cost effective than using the armature as a sabot for another projectile. This means railgun and coilgun rounds are restricted to highly conductive and highly magnetic materials respectively.

The bullets need to be cylindrical because they are launched from a tube, but they need not be aerodynamic in space. This means any sort of shape is viable in space, not just a bullet or thin penetrator. Fat blocky bullets are a viable shape, as are launching thin plates, flat side to target.

Given that aerodynamics is not a concern, what is the ideal shape of a bullet in space?

A fin stabilized Kinetic Energy Penetrator.

 

The answer is rather complicated. Certain relations are obvious though. For instance, a thinner shape applies a greater amount of pressure, as the energy is concentrated into a smaller area, so it seems like thin penetrators would be ideal.

However, there are two issues with that.

One is that Whipple Shields shatter thinner projectiles easier. Whipple Shields are often judged primarily by their critical diameter. This is the maximum diameter of projectile that they can be hit with and still successfully shatter or vaporize the projectile so that it causes no major damage. Obviously, material properties and impact velocity are both important, but projectile diameter is the main factor. Thus, thin penetrators are often not really worth the extra damage since Whipple Shields are ubiquitous.

A single-stage and a multi-stage Whipple Shield after impact.

Conversely, high velocity projectiles can sometimes be too effective. Indeed, given a large coilgun, shooting extremely high mass, high velocity rounds, the bullets can often blast straight through the initial Whipple Shields, straight through the main bulkhead, through several filled propellant tanks, out the external bulkhead and Whipple Shield, and finally off into space again.

Because only the crew compartments are pressurized, a spacecraft can suffer complete penetration and still keep trucking at 100% effectiveness. Spacecrafts can even get blasted in half and both halves can still remain reasonably effective (assuming each half still has a functioning crew and powerplant). Or into thirds, or fourths, and so on.

Cut in half but still threatening. Probably not for much longer though.

This is one reason why heavy redundancy in spacecrafts is necessary. A single lucky shot can immediately disable a ship if there is only one crew compartment.

On the other hand, one of my alpha testers went a different route. Rather than a single large capital ship with multiple redundancies, he preferred tons of tiny capital ships with zero redundancy. Either solution works, and has different pros and cons. More on this in a later post.

But back to projectiles being too effective. A projectile works best if it can penetrate the outer Whipple Shield and bulkhead, but is stopped there. That way, it can ricochet around, or if it shatters into plasma, it can inflict the most damage on the internals. In a sense, a larger area of effect is more important than simply raw damage.

Not only that, a projectile which passes straight through a ship fails to transfer much of its momentum to that ship, while a projectile that hits inelastically transfers all of its momentum. With very massive and very fast projectiles, inelastically hitting can cause tremendous torques on the impacted ship. Ships that spin out lose their carefully aligned targeting, and require precious seconds to reorient, which can mean life or death in a battle.

Or if the ship is particularly small, fast spins will splatter the crew against the inside of their crew compartments. This is actually one reason why I try to keep the crew modules near the center of ship mass, to reduce the torque on the crew in such a scenario.

Of course, if you don’t have enough power behind your bullets, you won’t penetrate the main bulkheads at all.

If your projectile is too powerful, then the obvious solution is to fire large, flat, plate shaped projectiles rather than thin penetrators. This reduces the pressure, and the damage area is increased. However, this can be tricky since large bores will mess with the performance characteristics of all projectile weapons.

Another solution is to split the projectile into smaller, less massive pieces right before hitting the target. Flak bursts were developed as anti-aircraft warfare, and they remain an effective way to distribute damage over a larger area of effect. A small explosive detonates the payload into a cylinder of fragments, and the detonation speed can be determined accurately (using the Gurney Equations). This allows you to have very fine grained control as to the size of this “sparse projectile”, and you can detonate it at different proximities to yield differently sized clouds of fragments.

A flak barrage slices through a Laser Frigate.

Other payloads possible in Children of a Dead Earth include explosive payloads and nuclear payloads. Nuclear tends to be a very powerful but expensive option, though due to the lack of atmosphere, their damage is incredible within a few meters, and then it falls of painfully fast. Explosives are similarly restricted to very small areas of effect but are much weaker, though they are fantastically cheap.

Should your projectile have thrusters? You can put thrusters on the projectiles you launch, and this can greatly increase their accuracy, however, the mass of the rocket engine and propellant is very costly. From what I found, barrages of thousands of small “dumb” projectiles tend to win out against tens of large “smart” projectiles, though I’d be interested if someone managed to optimize them to be competitive.

Often, a laser battery can effectively point defense tens of smart rounds, but against thousands of incoming bullets, no laser battery can keep up. Generally, against point defense, either you saturate them with a storm of tiny bullets, or you launch full blown missiles with heavy armor and large delta-v stores to get through.

Railgun point defense against a salvo of armored missiles. The missiles and their exhaust plumes are too small and dark to see, so they are each highlighted by the green circle.

There is another interesting aspect of projectiles that is often overlooked. Muzzle velocity is often optimized to be as high as possible. It increases the range and the impact damage. And even if it is too damaging, increasing the area reduces the damage without sacrificing range. It seems velocity should always be maximized.

Yet the equations for damage on Whipple Shields and Bulkheads are very nonlinear, and they have very different damage responses between hypervelocity and hypovelocity impacts. Indeed, Whipple Shields lose effectiveness for low velocity impacts, as the projectiles suffer little to no break up at low velocities.

Whipple Shields perform the worst between the Ballistic Range and the Shatter Range, which is approximately 3 km/s.

This is one particular case where conventional guns and their low muzzle velocity are actually desired. When the enemy is packing multiple and/or stuffed Whipple Shields optimized against high velocity railguns and coilguns, low velocity conventional guns tend to be the trump card. This is one case of many where drones, which usually carry conventional guns, tend to make short work of the enemy.

Space Guns

In the prior post, Misconceptions about Space Warfare, combat was roughly explored.

The general idea was that missiles and drones dominate long range combat since given enough delta-v, they can go anywhere a capital ship can go. Projectile weapons tend to dominate mid range combat, when capital ships or drones are tens or hundreds of kilometers away. And finally, lasers dominate short range, but also see use for mid range precision damage.

What it’s like on the receiving end of a drone projectile barrage. The occasional ricochet is also physically based.

Today, we’ll explore projectile weapons. The big three projectile launchers used most are Conventional Guns, Railguns, and Coilguns. There are also Linear Induction Motors used (railguns are technically a specialization of Linear Motors), which do not see major use aside from electromagnetic catapulting.

At their core, projectile weapons are concerned with two things: how big of a projectile it can launch, and how fast it can launched.

However, there are a multitude of other considerations as well. Mass. Cost. Size. Power Consumption. Cooling speed and temperature. Turning speed and angle. Armor against enemy attacks. Ammunition mass, cost, volume, and volatility. These are all accounted for in Children of a Dead Earth.

Firing a railgun. Ganymede in the background.

Before we contrast our three weapons, let’s start with commonalities.

All three weapon designs end up being tubular shaped, and accelerate their projectiles down that tube. This means these weapons are Cantilever Beams, or beams supported at one end, and as such, they will vibrate upon firing, causing inaccuracy and possibly shattering the weapon if the stress is too great. This is one limitation alluded to in a previous post (Origin Stories).

Another consideration is recoil, which all weapons must have, lest they violate conservation of momentum. Recoil stresses can also damage the weapon, and must be accounted for. Unless you use a Recoilless Rifle. Recoilless rifles have the issue that they need an exit pathway for the exhaust gases, which is tricky to make work in a large spacecraft, especially if the weapon is turreted.

Diagram of a recoilless rifle.

Note: Recoilless railguns or recoilless coilguns have never been attempted, but they are hypothetically possible, if you wish to eject the rails or the coils. That would likely be more expensive than what it’s worth, however.

A final concern is cooling. All of these weapon designs can use simple radiative cooling effectively in space to cool down, letting their long, exposed barrels radiate away all their excess heat. This is actually quite effective, and it is uncommon for projectile weapons to require additional radiators beyond their own gun barrel (unless you count the reactors powering them, which is a different story).

Now the differences.

Conventional guns detonate an explosive, and use the expansion of gases from that combustion reaction to accelerate a projectile down the tube. It’s more or less a combustion rocket engine with a bullet stopping it up. The tube is nothing more than a container to keep the gases in. As a result, the tube is cheap, the explosive ammunition is cheap, and no external power is needed. The downsides are lower muzzle velocities (less than 2 km/s usually) and the ammunition is very volatile.

An ammo bay explodes, tearing the capital ship in half. Note the explosion is faint and spherical. Explosions in space lose all brightness and color microseconds after combusting.

Volatile ammunition is a problem not just for when your ammo bays get hit, but for lasers as well. Precision lasers love conventional guns, as they can heat up the tube, prematurely detonating the round, and also potentially shattering the weakened gun barrel in the process.

Railguns run current through a pair of rails with a sliding armature between them, and the Lorentz Force that results from the current loop accelerates the projectile armature. They tend to have much higher muzzle velocities (<10 km/s) and nonvolatile ammunition. On the other hand, they require huge power draws, and the rails/barrel tend to be much more expensive and massive. Due to the way the rails ablate from heat and friction, railguns excel with smaller projectiles, and suffer with larger ones. All things considered, smaller projectiles are easier to make more accurate.

Designing a powerful 13 MW coilgun.

Coilguns run current through a series of loops, and use the magnetic field that results from these current loops to accelerate a magnetic armature down the barrel. They tend to have comparably high muzzle velocities as railguns, and also have nonvolatile ammunition. Their downsides are huge power draws again, but the coils/barrel tends to be somewhat cheaper and less massive than railguns. On the flip side, the ammunition is usually very expensive (unless you want to use cheap magnetic material like Iron, which yields much lower exit velocities compared to exotic stuff like Magnetic Metal Glass). In stark contrast to railguns, coilgun projectiles excel with larger projectiles, and suffer with smaller ones. This is due to Magnetic Saturation, where projectiles become saturated, and begin accelerating much slower, and it can only really be fought by using more and more massive projectiles (longer barrels do not help).

In a way, the three weapons tend to have their own niche in space warfare.

Conventional guns are cheap, and perfect for putting on disposable drones and small crafts without huge power supplies. Also, small crafts will be fast enough to get into range, as conventional guns have lower exit velocities and thus shorter ranges.

Conventional guns are cheap, low power, and small, which makes them the ideal weapon for small drones. Ceres in the background.

Railguns and Coilguns both have comparable exit velocities and power consumptions, much higher than conventional guns, and they dominate the capital ship battle space.

Railgun projectiles, though, tend to be smaller, less damaging, yet more accurate. This makes railguns the main point defense projectile system against drones and missiles (though lasers tend to beat them out against drones). Railguns also enjoy prominent use against enemy capital ships, great for perforating Whipple Shields and wearing down main bulkheads. The main autocannons in any capital ship engagement.

Coilguns, with their expensive and massive projectiles, tend to be limited to select ships which can afford the mass of their weapons. They form the inaccurate but devastating heavy hitters of capital ship combat.

These are the main constituents of mid to close range combat. There are a few projectile weapon technologies that were passed over for various reasons, but should be mentioned here.

A two stage light gas gun. Much bulkier than its electromagnetic brethren.

Light Gas Guns are a weapon which is capable of reaching similar exit velocities as railguns and coilguns. They are based on the principle that the speed of sound in a light gas (like hydrogen) is much higher than the speed of sound in air. With that in mind, a projectile can be accelerated at the speed of sound in the light gas using an explosive piston compressing that gas. In a sense, a light gas gun is like a spring airgun, only it uses a light gas instead of air. They also have none of the high power requirements of railguns or coilguns.

The downsides of light gas guns are their large size, and large and volatile ammunition. Each round launched requires not just explosives to hit the piston, but also a significant amount of light gas to accelerate it. As earlier posts pointed out (Gasping for Fumes), light gases like hydrogen have terrible densities, requiring huge volumes. Your ammo bay, in addition to exploding if hit, is going to be prohibitively large, making light gas guns not particularly viable for space warfare.

A Ram Accelerator

Ram Accelerators are weapons which launch a projectile supersonically into a tube of combustable gases. Using scramjet technology, the weapon will accelerate even faster through the tube of gases. It has the advantages of a conventional gun (cheap, low power) with muzzle velocities comparable to railguns and coilguns. However, it requires additional combusting gases with each firing, giving it similar problems to light gas guns.

An Explosively Formed Penetrator.

Explosively Formed Penetators are modern day weapons (they currently see heavy use in Iraq as IEDs) which uses a huge amount of explosives shaped in a lens to form a jet of molten metal and launch it at a target. Although it is primarily used as a warhead (and referred to as a Shaped Charge in that case), it can be used as a long range weapon. It is competitive with coilgun and railgun muzzle velocities, at the expense of only being able to shoot an explosively shaped projectile, meaning no payloads can be used with this. One major issue is the vulnerable ammo bay, which is like conventional gun’s ammo bay, but much worse. One hit, and the bay will have enough explosives to instantly shred the entire ship apart.

The other major flaw is that this weapon is that it’s absolute laser bait. The weapon is large, and the explosives are only covered by a thin coating of material, which makes for an easy precision laser hit. Because the explosives must be detonated in the correct manner, a laser-induced detonation is likely to severely damage the weapon as soon as any protective armor is pulled back.

Helical Railguns are a cross between a coilgun and a railgun. These systems have very little literature written on them, and the technology does not exist in a practical form, nor have their limitations and promises been studied heavily.

Nuclear Launched Projectiles are a technology where nuclear detonations are used to fling projectiles at a target (one test yielded a whopping 66 km/s). The main problem is that this requires the gun to be very far away from your capital ships, a single-shot drone essentially. Very little research has been done into this sort of weapon, so its actual viability for warfare is unclear. It is likely to be extremely cost ineffective.

A Voitenko Compressor, the only known practical method for generating enormous velocities.

Finally, Voitenko Compressors are guns which uses explosives to shape a gas into a shockwave to launches projectiles at enormous velocities, 60 km/s or higher. It was developed in the 1960s but little progress has been made with it, as a firing of it destroys the entire weapon, as well anything surrounding it. This relegates its use to a single-shot drone, once again, if these problems can’t be resolved. In the future, it could end up being the most powerful projectile ever developed, but currently, it is not a viable technology.

That was a small survey of possible future technologies, and most were not implemented because Children of a Dead Earth is near future. Far future technologies do not have the same rigorous application of engineering analysis, and so there no data on these technologies’ limitations, scaling laws, or true performance.

But what do we actually shoot? There’s more to what you shoot than simply mass, even for small weapons. Even if you’re not launching a payload, or a small gyrojet, or even a full blown missile, the shape and material of your projectile still make a big difference on how it will damage the enemy. We’ll explore these in a future post.

 

Gasping for Fumes

Finally we take a look at which propellant we should use for our rocket motor here. As mentioned in earlier posts, the two prime candidates for near future warship propulsion are the combustion rocket, and solid core Nuclear Thermal Rocket (NTR).

NERVA, the first Nuclear Thermal Rocket ever made, was developed in the 1970s. Later NTR designs have since improved on the concept.

Some reminders. Combustion rockets tend to achieve up to 5 km/s of exhaust velocity, and NTRs achieve almost twice that at their best. At the same time, NTRs suffer from lower thrust generally. NTRs in Children of a Dead Earth generally achieve around 3000 K temperatures in their reactor, limited by the materials that make up the core. Combustion rockets can achieve greater temperatures, but it’s wholly dependent upon the reaction used and the stoichiometric mixture ratio of the propellants (if using a multi-propellant reaction).

A popular combustion rocket is the LOX/LH2 engine, which uses liquid oxygen and liquid hydrogen to achieve almost 3000 K as well (assuming a 1:1 mixture ratio). This is the main engine of the space shuttle orbiter, and I’ll refer it to primarily when discussing combustion rockets, though later we’ll explore its limitations, and switch to different reactions.

The Space Shuttle main engines, LOX/LH2 combustion rockets.

Looking at the energy densities of nuclear energy versus chemical energy, one comes to the realization that nuclear power is roughly 600,000 more energy dense than hydrogen. So how on earth is a hydrogen combustion rocket even remotely comparable to a nuclear rocket?

After all, remember the rocket power equation:

Where is the Thrust, is the exhaust velocity, and is the power. If you increase the power by 600,000, either the thrust or the exhaust velocity must also increase by 600,000.

The trouble comes with releasing that power all at once. We have the ability to do so: it’s called a nuclear bomb. However, releasing it in a way that we can control is difficult, and must be done with a nuclear reactor. (This is one reason why the theoretical Nuclear Salt Water Rocket is so powerful: it tries to unlock that 600,000x power factor and still control it.)

A nuclear reactor’s rate of energy release can be seen through how high the temperature of the core can get. This means that between a NTR with a chamber temperature of 3000 K and a combustion rocket with a chamber temperature of 3000K, if they have identical mass flow rates, they must have identical rocket power.

Three different ships with three different exhaust plumes. From the top, methane NTR, water NTR, combustion rocket. The exhaust plume shape and size is physically based, deriving from refractive index spectra data and gas expansion calculations. Note that the water NTR’s exhaust plume is invisible.

Mass flow rate is how fast you can feed propellant into the rocket, which is governed by the turbopump injector you use to feed the rocket. The flow rate increases with pump size and with pump speed, and in general, is the same between an NTR and a combustion rocket.

This means, given an NTR and a combustion rocket of similar sizes and similar temperatures, the total power is roughly the same. And if we assume the exhaust velocity of the NTR is roughly twice that of the combustion rocket, the thrust of the NTR must be roughly half that of the combustion rocket. By extension, if the NTR has the same exhaust velocity as the combustion rocket, then the thrust must be the same.

A more direct way to see this is to look at the rocket thrust equation:

Where is the thrust, is the mass flow rate, and is the exhaust velocity. It’s obvious from this that given a constant mass flow rate, exhaust velocity and thrust are inversely proportional. On the other hand, in order to increase your rocket’s thrust, you simply need to increase the mass flow rate by using a bigger turbopump.

Essentially, this means the biggest advantage of NTRs, their high exhaust velocity, is the root cause of their lower thrust. Additionally, NTRs which do not have this advantage, the high exhaust velocities, have comparable thrust as combustion rockets!

List of NTRs, showing their propellants and their exhaust velocities. You can also go for more exotic propellants not listed here if you so desire.

In Children of a Dead Earth, Methane is the primary propellant used, because it achieves slightly better exhaust velocities than the best combustion rockets, which means in terms of thrust, it’s only slightly worse than combustion rockets. Decane and Water are also other NTR propellants that see heavy use.

But at that point, is there a purpose to using NTRs at all? If we only use NTRs that yield roughly similar stats to combustion rockets, why not just go with combustion rockets altogether? After all, combustion rockets are cheaper, don’t spew neutron radiation, and are somewhat less massive.

The trouble with combustion rockets, particularly the LOX/LH2 rocket, is the propellants. As mentioned in the previous post (Slosh Baffles), each propellant tank has an ultimate mass ratio ceiling. Roughly speaking, higher density propellants have higher allowed mass ratios. Given standard tank materials, water has an excellent mass ratio ceiling (in the hundreds), while hydrogen has an awful mass ratio limit (< 10 generally).

When using a bipropellant (like LOX/LH2), this mass ratio limit is primarily governed by the worst propellant. So in the case of LOX/LH2, the mass ratio limit is extremely low, because hydrogen’s mass ratio limit is low. Compare that to a Water NTR. A Water NTR will achieve comparable exhaust velocities and thrusts, but water is very high density compared to hydrogen, allowing much higher mass ratios.

On top of this, high density propellants allow your ships to be much smaller, making them much harder to hit in combat, and as indicted in earlier posts, minimizing your targetable surface area is critical.

A drone’s internals consists basically of propellant tanks and a rocket, emphasizing just how critical propellant density is towards reducing the targetable surface area.

Much more dense chemical propellants are needed to compete with the mass ratio limits. At this point, we have to discard the assumption that we are using the LOX/LH2 reaction. However, when looking into different chemical reactions, one finds that more dense chemical propellants tend to yield much higher exhaust molar mass.

In thermal rockets, the exhaust velocity is based primarily upon the temperature and the molar mass. Chemical reactions that have competitive or better mass ratio limits tend to yield somewhat lower exhaust velocities.

On the flip side, combustion rockets with certain reactions (particularly those involving fluorine) can achieve greater chamber temperatures than NTRs using clever cooling techniques not viable for NTRs. This means the total power of these rockets exceeds that of solid core NTRs. However, they tend to have low exhaust velocities once again, which means the power manifests as much higher thrusts.

Finally, what about the costs of propellants? Unlike just about every other equation in Children of a Dead Earth, determining the cost of something has no hard and fast rules. As a result, propellant costs are estimated primarily based on solar abundance, and on ease of extraction from common celestial bodies. In this way, common NTR propellants tend to be quite cheap. Combustion rockets with high density propellants end up being much more expensive comparatively.

Solar abundance chart. Recall that Children of a Dead Earth is set entirely in space, which means that Solar abundance is used, not Terran abundance, which has a different chart.

So where does this leave us?

If you want thrust, thrust, thrust, you should go with combustion rockets with high density propellants. Find a reaction with a high chamber temperature and a low exhaust velocity. The high density propellants might comparatively pricey against NTR propellants, though. This sort of drive is generally what most drones and smaller capital ships in Children of a Dead Earth use.

If you want high thrust but still want a reasonable amount of delta-v, NTRs tend to win out with certain propellants like Methane or Decane. This is what ended up going on most large capital ships. These drives tend to be the good-at-everything, excel-at-nothing choice.

And if you want middling thrust and an even higher delta-v, go all the way and grab a Hydrogen Deuteride NTR. Very few ships ended up falling into this use case, though.

Finally, if you want cheap, go for a monopropellant combustion rocket. Good thrust, awful exhaust velocity, but cheaper than dirt. This is what most small, disposable missiles use in game.

Nitromethane rockets. Cheap, light, tiny, and decent thrust. The nozzle is completely removed to save on mass, at the price of poorer thrust and exhaust velocity.

And of course, if thrust is totally irrelevant to you, maybe go for an ion thruster. Only a real option if you’re making a non-combat ship and don’t ever plan to dodge. And if you are okay with taking years to get anywhere.

One final note: It may surprise some readers to find that Hydrogen Deuteride () NTRs performs better (9.1 km/s) than pure Hydrogen NTRs (9.0 km/s), especially considering that Hydrogen () has a lower molar mass than Hydrogen Deuteride. This surprised me when I saw it as well.

As it turns out, the Gibbs free energy of formation of monatomic Deuterium is lower than that of monatomic Hydrogen, which yields a much lower dissociation temperature. At 3000 K, dissociation is less than 1%, while dissociation is nearly 100%, yielding higher exhaust velocities. As a result, is both denser (has a higher mass ratio limit) than and has a higher exhaust velocity, making it better in nearly every way. The only real advantage is that is slightly cheaper than .

And there you have an analysis of the major near future rocket engines that would see use in space warfare.

The choices allowed when designing your own rocket cover an enormous breadth of possibilities.

In the end, however, I am eager to see what sort of rockets that the players of Children of a Dead Earth can come up. Everything from the propellants to the stoichiometric mixture ratio, to the dimensions and shape of the rocket nozzle, to the turbopump injector attributes are editable in game. There are likely plenty of unexplored designs here that may beat out the designs I’ve made.

Slosh Baffles

So much time is spent discussing rocket engines that one of the most important parts of a rocket is glossed over: the propellant tanks. A significant amount of engineering goes into them, despite their simple appearance.

A rocket’s liquid propellant tank involves a number of considerations, such as propellant boil off, corrosion of the tank material, cryogenic insulation, slosh compensation, and pressurization. In space, without one g of gravity constantly pushing down, simply getting the propellant to the engine is a problem, since there is no force pushing the propellant into the rocket’s thrust chamber.

All of those issues must be dealt with using the least amount of mass, because of the rocket equation.

NASA stopped painting the space shuttle’s external tank white after two launches and saved on roughly 272 kg of dry mass.

Indeed, propellant tanks tend to be one of the largest contributors of mass to a spacecraft. An oft made comparison is that rocket propellant tank walls tend to be proportionally thinner than aluminum cans in order to skimp on mass. In Children of a Dead Earth, armor tends to beat out propellant tanks in terms of mass, which immediately begs the question: why don’t we use a Monocoque design?

A Monocoque design builds the propellant tank into the outer skin of the spacecraft, rather than having separate propellant tanks at all, and it is used by a number of rockets in modern times, such as SpaceX’s Falcon 1. Thus, armor doubles as propellant tank as well.

 

The Saturn V used a semi-monocoque design.

However, when a propellant tank suffers an external force such as that from a projectile, a water hammer, or a fluid shockwave forms within the tank, which can and usually will destroy the propellant tank. Thus, a monocoque propellant tank need not even be penetrated to be disabled. Enemies can simply hit the armor of the spacecraft hard enough to trigger a water hammer, and never even have to get close to penetrating the armor to render the spacecraft unable to move.

As a result, propellant tanks are kept separate from the armor skin. It costs more mass, but not significantly more, because it means the propellant tanks can be made much thinner.

Since Children of a Dead Earth takes place entirely in space without gravity, getting the propellant from the tanks into the rocket engine doesn’t happen automatically. There are a number of solutions to this issue, from ullage rockets (small solid fuel rockets designed to push the spacecraft forward, forcing the liquid propellant to the rear of the craft) to pressure diaphragms to piston expulsion devices.

 

Designs for both various pressurized diaphragms and a pressurized piston.

 

In Children of a Dead Earth, surface tension devices, or systems which use the surface tension of the propellant to pull it towards the engine, in tandem with a turbopump injector are used. They do not need the additional pressurized gas that pressure diaphragms require, and the turbopump feed needs only slight pressurization of the tanks, yielding thinner walls.

Several designs of turbopump fed bipropellant rockets. Nuclear Thermal Rocket designs are much simpler, requiring a simple propellant pump, and using an external power source rather than a turbine.

The lower pressure of the propellant tank also is valuable for avoiding water hammers for when the spacecraft undergoes rapid acceleration. Low pressure tanks also makes it easier to compensate for slosh effects with anti-slosh baffles within the tank.

On top of those considerations, cryogenic propellants may need to be insulated, although this is much less of a problem in space, as spacecrafts are not built in atmosphere, and so there is no convection of room temperature air always around the craft. Some propellants are corrosive to a lot of materials, and can only be stored in propellant tanks of certain materials. Finally, cryogenic propellants boil away at a slow but steady rate, and this too needs to be taken into account.

Assembly of the first stage of the Saturn V.

A last note on tank mass. Spherical tanks once again save the most mass, however, cylinders fit much better in cylindrical spacecrafts (discussed in blog post Why Does it Look Like That? (Part 2)), so capsule shaped propellant tanks are used.

All in all, there are a lot of details to worry about, and they all add mass, which is very troublesome for any spacecraft designer. After all, recall the rocket equation:

Where is the final delta-v of your spacecraft, is the rocket engine’s exhaust velocity, and is the mass ratio, or the wet mass divided by the dry mass. Recall that the wet mass is the total mass of the spacecraft including propellant, and the dry mass is the total mass except for the propellant.

In a previous blog post, Burn Rockets Burn, I went over the fact that the only drives with reasonable thrust for space combat are chemical propulsion and nuclear propulsion. In our case, combustion rockets or solid core nuclear thermal rockets. This limits your exhaust velocity to single digits of km/s. Also recall that while thrust scales up with the number of engines, exhaust velocity remains constant.

This means that the only way to squeeze out any more delta-v for your craft is by increasing your mass ratio. In particular, reducing your dry mass, or adding more and more propellant mass. Assuming you’ve reduced your dry mass as much as possible, getting more and more delta-v is simply a matter of adding enormous amounts of propellant tanks.

Since the delta-v scales with the logarithm of the mass ratio, consider this example. Suppose you have a spacecraft with an exhaust velocity of 5 km/s, either an excellent chemical rocket, or a middling nuclear thermal rocket. A mass ratio of (Euler’s number, ~2.7) will give you 5 km/s of delta-v. To get twice that, 10 km/s, you need a mass ratio of (~7.4), and to get three times that, 15 km/s, you need a mass ratio of (~20).

To make things less abstract, remember that a mass ratio of 20 means your spacecraft is 19 parts propellant, 1 part actual spacecraft. At that point, your actual spacecraft will be ballooning in size, because even the densest propellants tend to be lower density than the actual alloys and ceramics of spacecraft components.

A methane tanker with a mass ratio of 29. Note that it is mostly just methane at this point (28 parts methane, 1 part spacecraft).

And how much delta-v do you need? Maneuvering in combat around a planet or high gravity moon, from what I’ve seen, requires around 5-10 km/s to remain effective in combat (for evading missiles, drones, and even the enemy fleet). Somewhat more is needed when planning interlunar transfers, and tens of km/s are needed for interplanetary traveling.

For anyone who has studied the rocket equation, this is all pretty elementary. However, there is one complication that appeared from the rocket equation which was not immediately apparent to me. Once you have a drive chosen, the exhaust velocity is absolute. Thus, to get more delta-v, you get a higher mass ratio, by adding more propellant.

But there is an ultimate limit to your mass ratio, and by extension, an ultimate limit to the delta-v of your spacecraft. Not only that, you can bump into that limit very quickly.

Most of my capital ships run Nuclear Thermal Rockets using Methane as a propellant (for reasons I’ll outline in later posts), which yields an exhaust velocity of about 6 km/s. I started making a tanker with the same engine to refuel my capital ship fleets, and I wanted them to have an enormously high delta-v in order to get just about anywhere. Yet, almost immediately, I started hitting a low delta-v ceiling, no matter how many propellant tanks I added.

This is because every propellant tank added has dry mass in addition to its propellant. Thus, each tank has it’s own separate mass ratio, and a spacecraft can never have a mass ratio that exceeds the mass ratio of its propellant tanks. This propellant tank mass ratio approaches very quickly, and it depends heavily on a number of different factors, primarily the propellant type, the tank material, and the aspect ratio of the tank.

Some numbers here. In game, I optimized Methane propellant tanks to yield a mass ratio of about 30, around 50 for Decane tanks, and several hundred for Water. Most propellants cap out at around 50. Given very exotic and expensive materials, this can be doubled or tripled, though this often runs into corrosion or insulation issues.

A hydrogen tank with a very high aspect ratio. High aspect ratios tend to yield better mass ratios. Despite this, hydrogen tanks tends to have abysmal mass ratio because of how low density hydrogen is. This particular tank has a mass ratio of 4.2.

So, given a Methane rocket with an exhaust velocity of 5 km/s, and an ultimate mass ratio of 25 from the propellant tanks, the most delta-v your spacecraft can ever conceivably have is about 16 km/s. Yikes! That spacecraft will never make any significant interplanetary journey unless there are copious fuel depots along the way.

This emphasizes just how critical propellant depots are in space travel, and especially in space warfare.

One final way to push these limits are through rocket staging, which involves discarding your propellant tanks after use. However, if your spacecraft is armored, this involves likely dumping off a lot of expensive armor as well. A better way to do this is to take a number of propellant tankers with you, and then scuttling them after you’ve drained them out.

In Children of a Dead Earth, this is the primary way to stage an interplanetary invasion. When there are no allied propellant depots along the way, one has to take a huge number of tankers along for the ride, and then simply scuttle them at various points along the way as they are depleted.

Whew! That’s all for propellant tanks! We didn’t even get to a comparison of propellants in this post. I’ll have to get to them in a later post, but for now, you have all the challenges involved with managing your propellant tanks in space warfare.

Fun with Orbital Mechanics

Children of a Dead Earth uses an N-Body Simulation to simulate its orbital mechanics. Most other games which simulate orbits use the much less accurate Patched Conic Approximation, and I’ll go into the details of why in this post.

What is the Patched Conic Approximation, first of all? The Patched Conic Approximation treats all orbits as ellipses around a celestial body. Then, when actually making thruster burns, the current ellipse is swapped out for a new elliptical trajectory. When making an exit from one orbit into the parent body’s orbit, a new ellipse around the parent body is swapped in for the child body.

A perfectly elliptical orbit, although it rotates slightly with each period.

As you might expect, this is rather inaccurate. Indeed, when plotting actual spacecraft trajectories, NASA starts with the Patched Conic Approximation to get a “napkin estimate” of the trajectory, and then they switch to using an N-Body Simulation when they actually need to calculate it precisely.

Originally, Children of a Dead Earth was supposed to use Patched Conics. However, I discarded them when I wrote a simple N-Body Simulator to compare them against, and found the Patched Conics diverge very heavily from the N-Body Simulator. It was also the right choice: Switching to an N-Body Simulator allows a wealth of new orbital features, such as Orbital Perturbation and Lagrange Points.

So what is an N-Body Simulation? It’s simply a simulation which takes into account all gravitational forces in the entire system (in my case, the entire solar system) and applies them at each time step with a numerical integrator. Children of a Dead Earth uses a Fourth Order Symplectic Integrator by Forest and Ruth.

An orbit around Mercury perturbed significantly by the Sun.

Orbital Perturbation is a phenomenon that only shows up in an N-Body Simulator, and it makes a world of difference. Perturbation is simply the effects of gravity from more bodies than just the primary orbited body. Patched Conics do not simulate perturbation because they are only concerned with the gravity of one body at a time.

When orbits can be perturbed, they lose their perfectly elliptical shape and become at best distorted, and at worse, completely unpredictable, losing all periodicity.

Some orbits become perturbed so much that they become utterly unpredictable, and don’t seem to behave like orbits at all.

Why is this important? Consider the following story, which happened to one of my Alpha playtesters. He had spent a lot of delta-v injecting into orbit around Oberon in the Uranian system, and didn’t have enough delta-v to rendezvous with the destination space station around Oberon. His injection orbit was highly out-of-plane and succeeding seemed hopeless. But instead of giving up, he simply disabled stationkeeping, letting his spacecraft enter a free falling trajectory. Using the orbital perturbation of Uranus, he allowed the planet to perturb his out-of-plane orbit, gradually flattening it out into an orbit coplanar with the target space station. Eventually, by simply letting gravity do the work over several orbital periods, he had an orbit which could rendezvous with the target with minimal delta-v usage.

Using orbital perturbation in combat around Ganymede.

In combat, using orbital perturbation to your advantage is another effective but difficult technique to use. Dropping into a low orbit is often a useful tactical choice, as it forces your opponent to expend copious amounts of delta-v. However, it reduces orbital perturbation of nearby bodies.

On the other hand, entering very high orbits causes combat speeds to slow heavily, yet it costs much less delta-v, and it greatly enhances orbital perturbation. A perturbed orbit is much harder for the enemy to intercept because of its unpredictability, and the enemy will have to expend much more delta-v to reach you while you let gravity pull you along.

Furthermore, techniques like Orbit Phasing, which is a very effective way to intercept enemies, get thrown out the window when your target stops stationkeeping and enters free fall. Intercepting the enemy requires much more care than using simple maneuvers. After all, Orbit Phasing and Hohmann Transfers were developed for the Patched Conics Approximation, and are much harder to pull off in an N-Body Simulation.

A propellant depot in a tight orbit around the Jupiter-Europa L4 Lagrange Point.

Lagrange Points are also simulated only through N-Body Simulations; Patched Conics fail to correctly simulate these. Lagrange Points are five or fewer points around each celestial body and its parent where an orbit that remains stable relative to both bodies. Children of a Dead Earth simulates all manner of Lagrange Point orbits, from simple circular ones to more exotic Tadpole Orbits.

A figure 8 orbit around Mercury’s fourth Lagrange Point, Sun-Mercury L4. This orbit is a tadpole orbit that is twisted on itself.

That’s all for the N-Body Simulator! There is one additional aspect of Children of a Dead Earth’s orbital mechanics that is unique, and that is the way it handles multiple frames of reference, however, that will be another full post in and of itself.

Origin Stories

Today I thought I’d break from the usual, and go into detail about how this project of mine came to be. As you know, it started with the question: “What would space warfare actually be like?” A lot of sources, mostly hard science fiction literature, have tried to answer that question at one point or another. Other sources, like the Atomic Rockets website, does a great job of detailing the ideas at a high level.

For me, though, I wanted a simulation, one that was actually based on real equations. This is because in my experience, whenever you develop system this complex, it tends to surprise you, and will often overturn your assumptions. And trust me, it has surprised me continuously throughout the project.

The project originally was going to be not nearly as detailed as it is today. The original project would use black boxes for technologies: a railgun would be a system with X mass, Y volume, Z exit velocity of a W mass armature. The details would be glossed over. That worked fine for existing chemical rocket designs, because I simply had to copy and paste the numbers cited for SpaceX’s or NASA’s rocket engines.

It all started with railguns, though. When I went to do the same for railguns, there was a problem. The field of modern military railguns is limited to a handful of actual railguns that have undergone testing and deemed viable. I could implement these particular railguns as black boxes as well by collecting all the data I could find on them.

Railgun developed by the US Navy. The flame behind the projectile is not propellant, but rather the oxygen being ignited by the projectile’s launching. In space, no such flame would occur.

But what I wanted was scaling relations. If I took this railgun design, and doubled the power consumption, could I double the exit velocity? If I doubled the rail length, would that double the exit velocity? Is it possible to assume a simple efficiency percent, and derive my exit velocity based on the input energy and armature mass?

This answer to these questions, as I later discovered, are No, No, and No.

What I was looking for was simple equations which would relate the mass, power consumption, exit velocity, and dimensions. If I had these, I could scale these weapons up or down in various ways depending on the situation. A small drone would need a low power, low mass railgun, while a capital ship might have a ship-sized railgun of incredible power. I was looking for simple (ideally linear) relations between these attributes of a railgun.

As it turns out, that is not possible. The equations are complex, highly nonlinear, and many were unsolvable unless using numerical integration.

But I still wanted scaling laws for railguns, so I pressed on.

I started with the lumped parameter model for railgun force:

Okay, simple enough. At this point, I thought I could still have a simple equation describe my railguns. All I need is the inductance and the current and I can integrate the force across the length of the rails to get the exit velocity.

First the inductance. Wikipedia gives a gross estimate for this, as well as a simple equation which estimates the inductance by treating the railgun as a pair of wires. I wasn’t too keen on the estimate nor the equation because I was interested in a railgun that was cylindrical bore, and this thesis conveniently had what I was looking for. It developed an inductance equation for a cylindrical bore railgun based on the railgun’s bore radius, rail length, and rail thickness. Perfect for developing scaling laws relating the railgun’s dimensions and mass to the exit velocity. The equation itself was derived in the next chapter of the thesis and is duplicated below (for a given rail opening angle of 40 degrees).

Where the rail separation, is the rail thickness, and the coefficients through are derived constants which can be found in the thesis itself.

It’s a hefty equation, but it remains constant for a given set of railgun dimensions. What’s more is that it provides a very direct scaling relation between the dimensions and the ultimate railgun performance. A highly nonlinear relation, but a relation nonetheless. Just what I was looking for.

For the current, I found there are a number of ways to get pulsed power through your railgun: batteries, capacitors, inductors, compulsators, flywheels, hydrodynamic generators. Or, you can ignore these entirely and use continuous power. Where you attach the power supply also very significantly affects the final force. You can attach your power supply at the start of the rails, and the current will fall off as the projectile accelerates down them, or you can attach it at the end, or anywhere in between. Not only that, various designs implement multiple power supplies which attach at separate points along the rails to keep the current high.

At this point, the number of design choices was starting to undergo a combinatorial explosion, so I ended up setting some of the choices in stone. Only capacitors were implemented for pulsed power, and I implemented continuous power as well. Also, I set the power supply to only attach at the start of the rails.

In any case, the current was derived in two different ways for both pulsed and continuous power, and we’ll go into pulsed power. Resistance of the railgun is found easily by using the resistivity and dimensions of the rail and armature material. The capacitor itself requires knowledge of the capacitor’s capacitance (obviously), and the railgun was treated as an RC circuit, with the rails and armature being the resistor.

The voltage of the circuit is found simply with:

Where is the voltage at a certain time,  is the initial voltage,  is the time, is the circuit’s resistance, and is the capacitance. From the voltage, the current can easily be calculated, and this current can be plugged back into the force equation.

There is one final wrinkle, though. The voltage relies on , the time of the system, and the resistance relies on , the distance along the rails. After some wrangling, I set the equation in terms of either or , but in either case, the integral ended up being non integrable.

Thus, I had to use numerical analysis to calculate the final exit velocity (specifically, I’m using a Fourth Order Runge Kutta method), and I finally had my exit velocity.

My inputs were the following values: Rail Bore Radius, Rail Thickness, Rail Length, Rail Material (for resistivity), Armature Material (for resistivity), Armature Mass, Capacitance, Power Consumption. Not bad. Capacitance is derived further, but that’s a whole other blog post. So what I finally end up with is a series of values that I can tweak in order to see just how the exit velocity turns out. Not only that, but because the dimensions of the railgun are enumerated, I now know the railgun size and using the material density, I have the mass of the railgun as well.

Design of a railgun. The inputs you can manipulate are on the right, the stats that result are on the left.

But we’re not done yet! These equations allow you to invent hypothetically ideal systems which can’t exist in real life. The missing link is thermal and mechanical stresses on the system. The following limitations are implemented and must be checked for in a railgun:

The railgun rails can melt if the temperature becomes too high. If you read through the thesis posted earlier, the temperature concentrates are certain points, and these points need to remain under the melting point of the material for the entire firing. Additionally, the armature itself suffers similar temperature excesses and must be accounted for. The rails ablate from thermal stresses occurring far below the melting points of the rail and armature materials, and close attention must be paid here as well.

The recoil stress of the railgun will push the rails apart, and the rails must be able to withstand this stress without deforming. The barrel itself can be treated as a cantilever beam and needs to be able to handle the cantilever beam deflection stress when it fires. The armature suffers significant stresses as it is accelerated down the rails as well, and needs to be able to withstand them, lest it shatter.

Also, the bulk temperature of the railgun increases with each firing, and the railgun needs to be able to dissipate this excess heat in a timely fashion either through a coolant loop using convective cooling, or radiatively, through the barrel into space itself. Finally, thermal expansion stress can cause both the rails or the armature to crack and needs to be dealt with.

This particular design has three issues with mechanical stress. These issues tend to crop up for crazy high exit velocities.

These limitations are all implemented, and will be covered in a later blog post, since I’ve rambled on long enough here.

But once the limitations are all enumerated, I finally had what I was looking for: scaling relations for railguns. Given simple inputs like rail length, armature mass, power consumption, and so on, I was able to get reasonably accurate metrics for the exit velocity of a railgun, in addition to much, much more.

So this is just one particular origin story of how Children of a Dead Earth came about, in particular, why the granularity of the simulation is the way it is. There will be more origin stories to follow, such as on how very disparate parts of the simulation came together.

Burn Rockets Burn

We’re long overdue for a post about the rocketry of the game itself, so here it is finally.

Reaction engines are the cornerstone of any exploration of space warfare. Zero-propellant drives such as solar sails, laser sails, electromagnetic tethers, and the like, are not explored by Children of a Dead Earth due to certain limitations, particularly thrust. As you’ll see soon enough, thrust ends up being a heavily limiting factor for space travel.

Design for a Nuclear Thermal Rocket, which is more or less a nuclear reactor jammed into the thrust chamber of a thermal rocket engine.

The primary drive of Children of a Dead Earth is the Solid Core Nuclear Thermal Rocket, though a number of other technologies are supported. Many futuristic and experimental technologies were not included because a full treatment of these technology’s limitations has been published in scientific literature. Implementing the basic equations for a technology’s abilities, without fully implementing the mechanical and thermal stresses of that technology, would be disingenuous towards the end goal of the game. From my perspective, only exploring what a technology can do without keeping tabs on what it can’t is no better than inventing fictitious technologies altogether.

But anyways, why is the Nuclear Thermal Rocket (NTR) the go to drive in use? If you’ve been following the blog, you’ll find that it’s constantly brought up that delta-v is the limiting factor on just about everything. And due to the rocket equation, the easiest way to get more delta-v is to get a better drive with a better exhaust velocity. Well designed Solid Core Nuclear Thermal Rockets achieve 4 – 9 km/s, better than chemical propulsion, but mediocre in comparison, for instance, to ion thrusters, which can achieve 100 km/s or more. Or if you go for laser propulsion, or fission sails, or many more options, you can achieve orders of magnitude better exhaust velocity.

Hey look, those Magnetoplasmadynamic Thrusters have great exhaust velocities. Why don’t we use them instead?

You can also scale up the thrust of a rocket, but not the exhaust velocity. If you stick two identical engines together, your thrust doubles, but your exhaust velocity stays constant. So isn’t exhaust velocity the most important attribute of an engine?

Not exactly. You can work with a mediocre exhaust velocity with a greater mass ratio (though this maxes out too, this will be discussed in future posts) and staging. Counterintuitively, trying to get around mediocre acceleration is actually far more difficult.

After implementing the Nuclear Thermal Rocket, I looked into ion thrusters, and settled on the Magnetoplasmadynamic (MPD) Thruster, because it had some of the highest thrust out of all of them, and thrust is quite nice for dodging in combat. I built a few thrusters in the megawatt range, tried them out on a few missions, and their limitations became immediately apparent.

Thrust, and by extension, acceleration, is not simply important for dodging in combat. Low accelerations not only prevent you from using standard orbital maneuvers like Hohmann Transfers or Orbit Phasing, they vastly increase burn time and ultimately travel time. Getting between planets, for instance, might require a longer burn time than the actual period of the planets themselves, years, or even decades! Getting cargo anywhere in the solar system was prohibitively slow. NTRs and chemical propulsion turned out to be far superior.

It doesn’t matter that you have tons of delta-v, if it takes you years or decades to use it all.

With combat spacecraft, it only got worse. The accelerations are so poor that orbital evasion maneuvers are impossible to execute against high-g missiles or anything else really. In range of weapons fire, enemy projectile range is limited primarily by the target’s areal cross section, and its acceleration. With accelerations as low as the MPD Thruster was yielding (micro-g’s at best, nano-g’s at worst), my warships were basically immobile, sitting ducks for the enemy. And I should emphasize: The MPD Thruster yields one of the highest thrusts of any of the ion drive designs.

Okay, though we can just crank up the power consumption, and get higher thrusts, right? You can actually, as long as you keep an eye on the various stresses of the design. In particular, Onset Phenomenon of MPD Thrusters gets rather nasty at megawatt levels of power.

Designing a MPD Thruster. Compare it to the NTR above. This MPD Thruster has 4 times the exhaust velocity, yet the NTR has over 10,000 times the thrust.

But more power requires more nuclear reactors, and more reactors require more heat radiators. The amount of heat radiators by mass became overwhelming, and reduced the spacecraft’s overall acceleration faster than adding more MPD Thrusters could increase it.

At this point, the Rocket Power equation (it’s further down in the link) should be pointed out. For a given amount of power, the thrust is inversely proportional to the exhaust velocity. This equation became very evident with MPD Thrusters. One could increase the mass flow of the engine (and thus, the thrust) at the cost of plasma excitation (and thus, exhaust velocity). The two quantities were directly opposed.

I designed a MPD Thruster with exhaust velocities comparable to NTRs, and found the thrust still lacking. NTRs had a rocket power in the multi-gigawatt range, and my MPD Thrusters were in the tens or hundreds of megawatts range. They’re both run via nuclear reactors, so why were MPD Thrusters so much worse in this regard?

It wasn’t until I designed resistojets powered by a nuclear reactor (Nuclear Electric Propulsion) that it hit me. The additional step between the nuclear power generation and actually utilizing this power is the problem. NTRs and Combustion Rockets expel most of their waste heat through the exhaust itself, while nuclear powered resistojets and MPD Thrusters must expel most of their their waste heat through heat radiators unconnected to the drive. Making a MPD Thruster or resistojet with the same power as NTRs requires a staggering amount of radiators while NTRs do not. Counting the mass of the radiators needed for such a high powered MPD Thruster into the drive’s total thrust-to-mass ratio yields abysmal ratios.

In fact, most drives suffer from this same limitation that NTRs and Combustion Rockets avoid. Only a few drives, like Nuclear Pulse Propulsion manage to sidestep the issue of requiring enormous amounts of radiators to have comparable power. But ion drives, and nearly all other high-exhaust-velocity counterparts, fall flat. As it turns out, thrust is hugely important to spacecraft.

It was at this point when it finally clicked for me why aerospace engineer Robert Zubrin, inventor of the Nuclear Salt Water Rocket, has long since called ion thrusters (in particular, VASIMR) a hoax. I personally wouldn’t call them hoaxes, but in order for them to be the future of space travel would require a hypothetical advance in technology to fix their glaring flaws. As it stands, ion thrusters don’t appear to be viable for any sort of bulk space transportation. For scouts and tiny probe spacecrafts, ion thrusters are great. But for moving cargo, passengers, and military ordnance around the solar systems, ion thrusters and electric propulsion simply aren’t going to cut it.

Leave it to Zubrin to conceive of an engine that requires continuously detonating nukes inside your rocket’s thrust chamber.

Extremely high thrust propulsion looks to be the way to go, unless the radiator limitations can be solved somehow. Discounting far future drives like antimatter engines, this cleanly kills off a huge portion of potential drives for bulk space travel: ion thrusters, most sails and tethers, electric thrusters, photon thrusters, fission fragment thrusters. All you are left with besides chemical propulsion is nuclear, nuclear, nuclear. Maybe I should’ve listened to Robert Zubrin from the start.

That’s a quick run through on the rocketry of the game, next time we’ll explore one of the most overlooked, yet extremely important parts about space travel: the propellant tanks themselves, as well as the pros and cons of different propellants to use. As it turns out, neither of these are as simply as you might imagine.