Supercriticality

One of the most complex parts of a spacecraft is the power supply, which usually takes the form of a nuclear reactor.

Cherenkov Radiation from a nuclear reactor core.

Nuclear fission is about 600,000 times more energy dense than the most energetic chemical power reactions, which very easily makes it the best power supply for space. In space, mass is a premium, so energy density is critical. Most capital ships use fission reactors to get their power.

Schematic of a Radioistope Thermoelectric Generator.

Similarly, Radioactive Decay runs about 15,000 times more energy dense than chemical reactions, which is why Radioisotope Thermoelectric Generators (RTGs) are the next best thing. Most drones and missiles with significant power needs use RTGs. Anything with lesser power needs simply use small batteries.

Chemical energy requires tremendous amounts of mass produce reasonable amounts of power, after which this mass is ejected. This makes it not very viable for space except as rocket propellant.

Solar panels in space. Beyond Earth, they rapidly lose effectiveness.

Solar power becomes more or less useless further away from the sun (at Jupiter, the irradiance is 30 times lower than that on Earth). They are also much harder to armor than radiators, making them a poor investment for space warships.

Beamed power suffers from the beam waist widening very quickly over distance, which limits its effectiveness to very low orbits around celestial bodies. This occurs even with a constellation of mirrors to extend the range. Beamed power similarly require receivers that can be damaged easily, and if they are to be used in close combat, they can’t be covered up, making beamed power fairly infeasible for warfare.

A Z Machine, a device for researching Inertial Confinement Fusion (ICF).

Fusion Power is a power source that could make all other sources obsolete if it can be developed. In its current state, it is too far future of a technology. An additional consideration about Fusion Power is that it, along with Fission Power, are not limited by energy density, unlike the other aforementioned power sources. While the other power sources are limited by not producing enough power, Fission and Fusion Power both generate more power than modern systems could ever dream of using. Fission Power is not limited by how much nuclear fuel you have, it is limited primarily by how large your radiators are. This means any limitations on Fission Power currently will still remain even if Fusion Power replaces it.

All of this means that the main power supply in Children of a Dead Earth is nuclear fission.

Cooling towers of a nuclear reactor. The actual reactor core is underground, and tiny compared to the machinery used to extract power from the core.

In Children of a Dead Earth, nuclear reactor cores are governed by the Six Factor Formula. This rather large and complex equation which determines the effective neutron multiplication factor. Given the masses of all the materials inside the core from the fuel to the moderator to the neutron poison to the coolant, the operational characteristics of the reactor can be determined. This means the rate at which a core achieves criticality or shuts down can be predicted, and it usually takes microseconds.

Given a working reactor core, the neutron flux of a reactor can be arbitrarily controlled. The neutron flux directly determines the amount of heat the reactor will produce, which means the reactor can arbitrarily control the heat produced, and by extension, the power produced.

These fission reactors are not limited by the Uranium-235 fuel (or Pu-238 or Am-242m, etc.) inside the core. In practice, the amount of nuclear fuel is minuscule compared to the rest of the reactor elements. This is why 3% enrichment of U-235 is actually quite reasonable for reactor fuel. Contrast this with nuclear weapons, where around 97% enrichment of U-235 is preferred.

The main power limit inside the core is how hot you can make it. And generally how much heat your reactor can withstand is dependent on how large you can make the reactor to reduce energy per unit area. Additionally, the design of your fuel makes somewhat of a difference, as fuels such as TRISO allow for a Pebble Bed Reactor design, which yields somewhat higher heat tolerances.

Cutaway of a TRISO pellet, showing various ceramic layers over a U-235 pebble.

The reason temperature is the limiting factor of a nuclear reactor, rather than the actual fuel mass, is that the energy density is so high that a nuclear reactor will never come close to unlocking all of the power of even a small amount of fuel mass. Nuclear reactor design mostly boils down to how much energy can be extracted from a tiny amount of nuclear fuel without melting to slag.

Thus, how much nuclear fuel is needed has nothing to do with how much power you need, and everything to do with whether or not your reactor can achieve a critical mass.

CANDU fuel bundles, another nuclear fuel design for heavy water reactors.

For this reason, using more or less energy dense nuclear fuels is basically pointless, as they all produce “too much”. The main difference between fuels is how they affect the neutron multiplication factor. Certain fuels, like Am-242m, can achieve a critical mass more easily, and thus, less nuclear fuel is needed. This means the reactor design might be made smaller for the same amount of power.

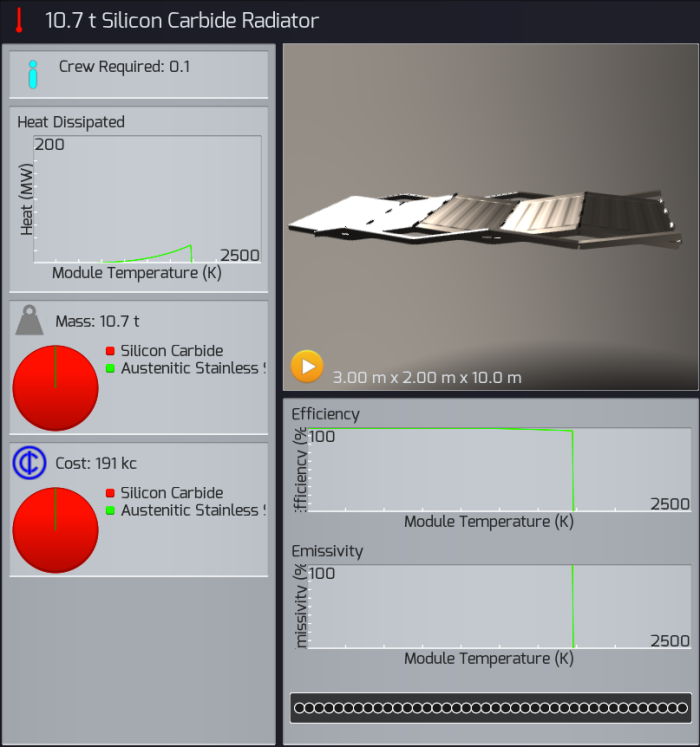
In practice, however, the mass of the radiators ultimately end up being the limiting factor on nuclear reactors.

Of course, simply creating an atomic pile and letting it spew neutrons and radioactive waste is not enough to produce power. Power needs to be extracted from the heat of these fast moving nuclear byproducts. A number of methods have been devised to do so.

The exposed turbine of a turboelectric nuclear reactor.

Turboelectric Fission Reactors involves letting the neutrons heat up the coolant and using the hot vaporized coolant to turn a turbine. This technique is the most common, being used in just about every nuclear reactor in the world. It requires a large turbine to effectively extract the heat, as well as plenty of coolant and turbomachinery to run it properly. Due to the size, it can take a while to warm up. Due to the mass and complexity, it generally is not used for spacecrafts.

Turboelectric Fission Reactors are heat engines, meaning they can never exceed the efficiency of a Carnot Cycle:

Where is the efficiency, is the cold temperature of the coolant prior to passing through the reactor, and is the hot temperature of the coolant after passing through the reactor.

As noted in Why does it look like that? (Part 3), the cold temperature needs to stay high because this is the temperature the radiators will cool the reactor at. Cold radiators function abysmally and require huge amounts of mass. Similarly, the hot temperature needs to stay low to prevent the systems from cracking from the thermal stress.

A thermoelectric reactor which produces 13.5 MW. Does not include radiators.

The sample reactor has a radiator temperature of 1200 K and 1688 K as the hot temperature. Using the above equation, this means the efficiency of that reactor can never exceed 29%, if it were theoretically perfect. In practice, the actual reactor runs at 22% efficiency.

On Earth, turboelectric reactors often quoted at running at 60% efficiency. This is possible because the cold temperature can be brought much lower if you are using conduction or convection to cool off the reactor. In space, using only radiators forces the cold temperature to be rather hot (> 1000 K usually) in order to keep the radiators from getting too large.

The SNAP-10A reactor, a thermoelectric reactor developed by the USA in the 60’s.

Thermoelectric Fission Reactors are heat engines as well. However, instead of passing the hot coolant through a turbine, it instead passes against as a thermocouple heat exchanger. It involves much less turbomachinery, and thus can be produced in much smaller sizes with much lower masses. On the flip side, it is often much further from the theoretical Carnot Cycle efficiency than turboelectric reactors. In space, it is the primary go-to reactor design due to its low mass, simple design, and cheap cost.

The TOPAZ nuclear reactor, a thermionic reactor developed by the Soviet Union and launched into space in the 80’s.

Thermionic Fission Reactors uses the concept that the flow of charge carriers (such as electrons) across a potential barrier can produce power. This flow of electrons is triggered thermally, and thus is set up very similarly to the way Thermoelectric Fission Reactors work. It is also a heat engine, and sees similar use in space as the thermoelectric fission reactor.

Fission Fragment Reactors do not use coolant at all, and instead extract power by decelerating the neutrons and radioactive waste products using a magnetohydrodynamic generator. This bypasses the Carnot Cycle entirely, allowing efficiencies estimated up to 90%, far greater than any of the previously mentioned heat engines. However, it is also the least developed of all the technologies, and to date, no working Fission Fragment Reactor has been produced.

Another picture of the Cherenkov Radiation of a nuclear reactor. Just because.

Since Children of a Dead Earth restricts itself to functioning technologies, this means nuclear reactors are restricted to Heat Engine designs. And due to the Carnot Cycle, the efficiency is forever limited by the cold temperature, or the radiator temperature.

Due to this restriction, the most massive part of a nuclear reactor is the radiators that accompany them. The power extraction machinery tends to be the next most massive piece, with the reactor core itself generally being negligible in terms of mass. On the flip side, the tiny amount of reactor fuel tends to be one of the most expensive parts of the entire system.

Stealth in Space

Few concepts of space warfare have inspired as much controversy (and hate mail) as discussing stealth in space, so I figured it’s time to have an article about that.

The bright Apollo 8 plume observed from Earth, as it makes a Trans-lunar Injection.

For starters, though, I’d recommend checking out Winchell Chung’s website, Atomic Rockets, which has an excellent discussion on this topic, aptly titled There Ain’t No Stealth in Space. I will summarize the main points about stealth here, but for an in-depth discussion of them, see the above link.

• Carefully scanning the entire celestial sphere takes 4 hours or less.
• Thruster burns of any drive with reasonable power can be detected all the way across the solar system (billions of km away).
• Even with engines cold, the heat from radiators attached to life support will be detectable at tens of millions of km away, which is still far too large to get any sort of surprise.
• Radiating heat in a single direction (away from the enemy) is easily defeated by fielding a number of tiny detector probes which idly coast about the system. Additionally, the narrower of a cone in which you radiate heat, the larger and larger of radiators you need to field. A 60 degree cone of radiation is roughly 10% as efficient, and it only gets worse the tighter of a cone you have.
• Making a huge burn and then trying to stealthily coast for months to the target is do-able, but as long as your enemy can track your first burn, they can very accurately predict where you’ll be as you coast across the solar system. And you still have to worry about radiating your heat for months.
• Decoys are only really viable on really short time scales, such as in combat. Over the long term, study of a decoy’s signature over time will reveal it’s true nature. It would need a power source and engine identical to the ship it’s trying to conceal, as well identical mass, otherwise the exhaust plume will behave differently. This means your decoy needs to be the same mass, same power, same engine as your real ship, so at that point, why not just build a real ship instead?

Anti-stealth detection measures was developed heavily during the cold war for detecting ICBMs. In space, without a horizon or an atmosphere, it’s far easier.

There are a few more points that are not mentioned but I get messaged about them a lot, so I’ll put them here.

• Hiding behind a planet to make a burn is not really feasible. All it takes is two detectors at opposite sides of this planet to catch this. In reality, a web of tiny, cheap detectors spread across the solar system will catch almost all such cases.
• A combat-ready ship will require very hot radiators for its nuclear powerplant for use in combat. If these radiators are going to be completely cold for the journey, they will suffer enormous thermal expansion stress when activated. In order to avoid this, very exotic and expensive materials for your radiators will be needed to get from 10 K to 1000 K without shattering. Not only that, your radiator armor will need to be similarly exotic, which means it will likely not be very good at armoring your radiators anyways.

Rocket exhaust plumes can be uncoupled from atmosphere using modern technology after some study. This step can be skipped in space.

Now there are plenty of dissenting views (as Atomic Rockets is good to point out, as well as rebuttals to the rebuttals). Certain partial solutions, such as using internal heatsinks, and so on, are pointed out, but they all are very limited.

Ultimately, stealth in space is somewhat possible, but current proposed solutions are either ridiculously expensive, impractical, or require you to accept limitations that defeat the purpose of stealth in the first place. Indeed, rather than consider it a ‘yes-or-no’ question, it’s simply a matter of how close you can get to the enemy before they detect you.

In practice, ‘how close’ generally means halfway across the solar system, with expensive stealth solutions reducing that distance only partially. Given this, Children of a Dead Earth runs with the assumption that stealth is not a reasonable military tactic for near future space warfare.

But let’s look at an example of possible stealth: replacing your main engine (nuclear rocket or combustion rocket) with a solar sail. Your exhaust plume is now nonexistent, but now you have to take decades to centuries deliver a military payload anywhere (troops or weaponry). Your best bet is to keep your payload very small if you want to get anywhere in reasonable time. And you still have to worry about your radiators.

Concept art of a solar sail. Abysmal thrust, and basically useless in the outer solar system, but it’s stealthy.

Suppose replace your crew module with basic electronics, and do away entirely with the crew and their hot radiators. This is reasonable for any short term space travel, but over the course of months where things can and will go wrong with the ship or the strategic situation, having a human element is necessary. Alternatively, if Strong AI can be developed, this is another possible solution, but this assumes that such an AI won’t require lots of power and heat to radiate as well.

A different idea to get around this problem is to put everyone in cryosleep and keep the ship basically frozen. Comes with a host of it’s own problems as well, chiefly that the technology does not exist yet.

Given a solar sail and crewless ‘dumb’ ships with miniature payloads, you can build ships that can sneak across the solar system and do very little. Such ships would be unable to respond to complex and unexpected tactical decisions, and would be very easy to outsmart, as well as easy to spoof with electronic warfare. They could perhaps be used as mines, given a tiny amount of a delta-v and a small nuclear payload.

Ironically, this specification of tiny, ‘dumb’ stealth crafts is exactly what you need to build a web of detectors scattered about the solar system. This means the field of cheap detectors you want spanning the solar system can be created stealthily.

The Hubble Space Telescope. Much smaller and cheaper versions can be scattered about the solar system stealthily if using solar sails.

Defensive stealth in space exists in full force. When you enter orbit of an the enemy’s planet, they might have an inordinate amount military hardware and spacecrafts hidden beneath the surface. But as soon as they launch, the secret is out.

This idea plays a major role in Children of a Dead Earth, as when the enemy drops into orbit around your planet, one must always be wary that the enemy fleet is simply trying to draw out your forces to get a tally on what you actually have. This constantly requires balancing of launching just enough firepower to deal with the enemy without revealing too much about one’s own reserves.

A Titan Missile Silo from the cold war. Similar silos could be littered across planets, moons, and asteroids with full fledged capital ships, ready to launch when the enemy enters low orbit.

The easiest way to conceal a large amount of military hardware for a long distance invasion is to hide it amongst commercial traffic. Of course, this requires complicity with the civilian traders, either bought with money or intimidation, but it is possible. And such perfidy also plays a key role in Children of a Dead Earth.

With that all in mind, I will admit that at the beginning of my project, I was dead set on getting stealth to work in space warfare. Ultimately, I came to the conclusion that while stealth in space is certainly possible, it is not feasible given mass, cost, and time constraints. If you want stealth, you need to pay the price of decades-long travel times, enormously massive ships, vastly reduced military effectiveness, or all of the above all at once.

At the beginning of the project, I did explore some more exotic solutions to stealth, but I ultimately wasn’t keen on implementing technologies that were not heavily reviewed and published in scientific articles. At some point though in future posts, I will go over all of the more ‘out there’ technologies I considered for all aspects of space warfare (like a hypothetical nuclear rocket which generates an exhaust plume at 30 K, for instance). Stay tuned!

Why does it look like that? (Part 3)

Previously, we examined why lasers and exhaust look they way they do, in addition to spacecrafts’ shapes. Now we’ll look more closely at one specific part of spacecrafts: the heat radiators.

Fleet Carrier cutaway, also showing all radiators glowing at peak temperature.

Heat radiators are necessary for spacecrafts in order to cool their internal systems. Nuclear reactors produce tremendous amounts of waste heat, and other subsystems produce smaller yet substantial amounts as well. Nuclear-enabled naval ships on Earth can cool their reactors via convection since they are sitting in an enormous bath of coolant already: the ocean. Aircraft and ground craft also have the air to use as coolant to constantly soak away heat.

No such solution exists in space. The lack of any sort of fluid medium in space prevents convective cooling, and there exists no solid material in space to support conductive cooling either. This leaves the one remaining method of cooling: radiation. All materials always radiate photons via Blackbody Radiation, and the amount and kind they do depends on the temperature: hotter materials emit much more energy.

This is where heat radiators come in. These are already in use on the ISS.

Heat radiators on the ISS on the right and bottom. Solar panels on the left.

They are flat panels with tiny pipes running through their entirety, pumping in scalding hot coolant through one side, and cooled off coolant out the other side. In this way, the radiators form a closed coolant loop with the system that needs cooling. Each set of radiators cools a different system, which is also why some radiators glow orange hot, some glow yellow hot, and some don’t even glow at all (well, they’re actually glowing in infrared, too cold for the visible spectrum).

Unfortunately, you can’t simply dump all of your systems’ coolant loops into a single loop and pipe them through a single enormous radiator because of the second law of thermodynamics. Closed thermodynamic systems will maximize entropy over time. Put another way, heat always flows from hot to cold.

This means that if you have a nuclear reactor running at 1000 K (degrees Kelvin) with its radiators dumping out heat at 1000 K, and you hook it up to a crew module running at 293 K, you have a problem. The crew module and nuclear reactor coolant loop will combine to yield a temperature partway between the two. This will still cool off the nuclear reactor, but then it heats up the crew module until the people inside are cooked.

Module design of a radiator. Silicon Carbide ceramic core with Stainless Steel finish.

Why are radiators shaped like that? Heat emitted is directly proportional to surface area, so flat plates are the most mass-efficient way to radiate heat: maximum surface area, minimum volume. The jagged shape is to allow them to be retracted inwards to temporarily reduce heat signature (if enemy missiles are homing on you) or to protect them from damage.

Certain other designs of radiators exist, but many of them have issues. Liquid droplet radiators use a liquid pumped between a sprayer and a collector. The liquid allows a much higher temperature since the boiling point of the material is the limiting temperature instead of the melting point for solid radiators. Problem with this is that temperature is by far not the limiting factor of radiators. Silicon Carbide and other similar refractory ceramics can be heated to excess of 3000 K without melting. Even more exotic materials, like Hafnium Carbide, can exceed 4000 K (For comparison, the Sun’s surface is 5778 K) without melting! Their material properties are weaker at that temperature, but they remain still usable as radiators, and as long as they are never dropped below a certain temperature, they will never crack from thermal expansion stress. For reasons I’ll outline below, the internal systems will never emit coolant hot enough to take advantage of these refractory materials’ high melting points.

Another kind of liquid radiator, the Belt Radiator.

The radiators can never be hotter than the system they cool due to the laws of thermodynamics. However, the nuclear reactors in game can reach up to 3000 K, yet the radiators rarely ever exceed half that. In fact, for one of the reactors used for power production only in game, the reactor core never exceeds 1688 K and the radiators radiate at 1200 K. This reactor’s design is shown below.

13 MW electric solid core nuclear reactor.

Why are the temperatures so low when the materials used can withstand temperatures twice as high? Two things: the machinery between the reactor core and the radiators all needs to be able to withstand this heat, and the system works best when the temperature drops.

The reactor uses a thermocouple to convert the heat gradient from the reactor into power (note that a turbine-powered system would have somewhat similar limitations). The thermocouple first must withstand the high temperatures. Thermocouples require materials with high Seebeck Coefficients, and these materials tend to have low melting points. On top of that, the high temperature difference involves very significant thermal expansion stress, which is also not something these materials are good at withstanding.

Secondly, thermocouples are most efficient when the temperature drops significantly across them. This yields an interesting optimization problem. If the temperature drop from reactor to thermocouple is high, then the temperature drop from the radiators to space must be low, and the reverse is true. Remember that radiators perform best when their temperature is high.

This means the more efficient the reactor is at producing power, the harder it is to cool the system. On the other hand, a low efficiency reactor is very good at cooling itself. This problem yields two different valuable qualities that are inversely proportional to each other, and no local maxima can be found for both simultaneously.

In the end, for the above system, the somewhat reasonable point for both properties was at 1688 K for the reactor and 1200 K for the radiators.

Color temperature of Blackbody radiators.

That 1200 K temperature is why the largest radiators on spacecrafts glow orange. In fact, you estimate the temperature of radiators by their color, and from that you could estimate their purpose.

What about inter-reflection? Inter-reflection of radiators is a problem, since the heat from one radiator can be re-absorbed into another. This is exacerbated by Kirchhoff’s Law of Thermal Radiation, which states that the emissivity and absorptivity of a material is identical for any given wavelength of light.

Tail end of a spacecraft, showing how radiators will re-absorb each other’s heat radiated to some degree.

Blackbody radiation emits not simply perpendicular to the emitting surface, but in a full hemisphere of directions. Note that the intensity does fall off with the cosine of the angle from the perpendicular, however, so emission is most intense perpendicular to the radiator, and it falls to zero directly parallel to the surface. This does mean that these radiators will suffer inter-reflection, which will reduce their total efficiency, but they still will do the job, and can still be placed next to each other at narrow angles to each other.

Finally, can these radiators be armored? The answer is yes, contrary to what other sources may claim. Radiators are simply panels with material with tubes hollowed out in them to pass coolant through. One can simply increase the panel thickness beyond the tubes to add monolithic armor, and the refractory nature of the radiator materials means they will remain very strong even at orange-hot temperatures.

But, thicker monolithic plating reduces the efficiency of the radiators, because it will negatively impact the Heat Transfer Coefficient of the convection-radiation system. Thus, this yields yet another optimization problem, with radiator protection being inversely proportional to radiator efficiency. One will generally find that the added mass and poorer efficiency is often a fair trade for radiators that can actually withstand a serious beating.

That’s all for radiators! Next time, we’ll look into moment-to-moment space combat itself.